当前位置:首页 » 其它 » 正文
-
引言
由于武汉疫情影响,大家都把自己隔离在家。最近网络流行一组来自“刘小兔爱画画”的漫画作品《看了这个逻辑关系图,才更清晰为何不让你随便外出了》。我们先回顾一下这组漫画:把现在的人群分为四类 A 、B、C、D。

A是有武汉接触史的人,目前分散于全国各地,容易找出来,现在已经找出来很多。
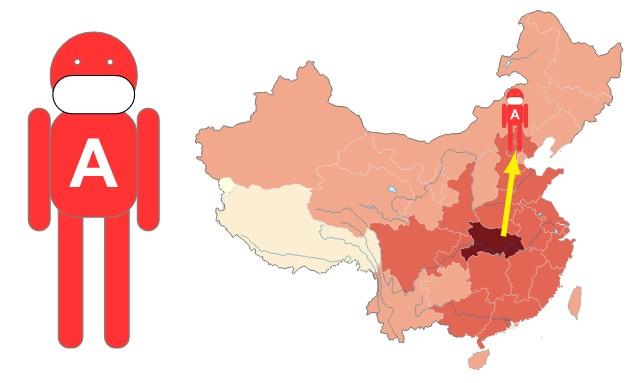
A 在公共场所遇到过素为平生绝不认识的B,A不知道B的存在,也不知道A的存在。
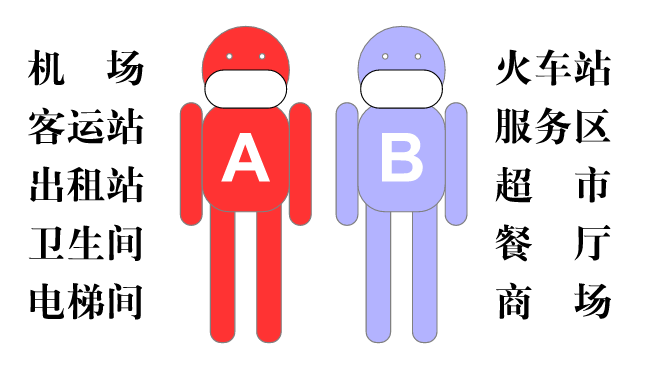
A到达目的地后接触了C ,无论接触了多少C , 这些 C都容易找。

官方已经找到了 A、 并对他们进行了隔离。
D是居家没有外出的人。
现在最大的隐患是 B,根本找不到,没有人知道谁是B ,自己也不知道自己是B。

D 只要出门,就有碰到B的可能性,自己也就是 2B (新的B) 了。
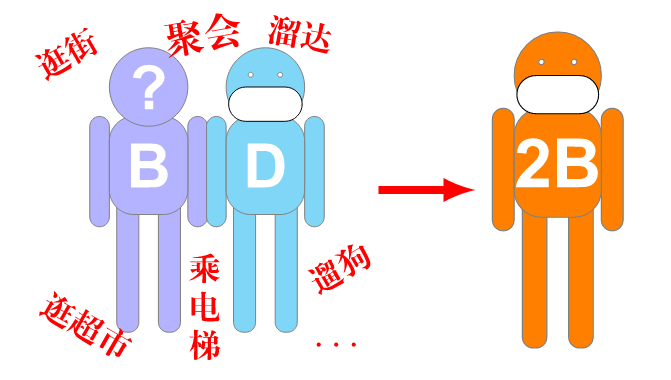
这组漫画非常生动地解释了肺炎的传染途径,以及为什么不要随便出门的原因。不过大模头已经快控制不住我技己了,相信你也很想出去逛逛。所以想知道要是随便出个门,突然变成一个“2B”的概率有多大?
模型
本文不考虑你是 A的情况。你是不是A,你有没有去过武汉,你是不是从武汉回来的,你心里没点哔数么?因此,你是不是 A不需要算,你自己心里清楚。
你身边有多少 A?
武汉市前市长周先旺表示:春节和疫情因素的影响,大概 500 多万(本文的计算中取 550万)人离开了(武汉)这座城市,还有将近 900 万人生活在这个城市[1]。
如果你生活在武汉,那么你生活的城市处处都是 ,本文不讨论这种情况。这种情况下请保护好你技己,做到不要成为 ,,,,其中 万。
那么除了还在武汉市内的 ,全国其它地区共有 550 万 。大数据 [2] 显示这 550 万中有近 450 万都去了湖北省内的其它城市。也就是说除了湖北省,全国其它省市大约有 100 万 。我们假设这 100 万 按人口比例均匀分布在全国所有人口中。本文假设你生活在北京,北京人口大约为 2500 万左右,约占全国总人口的 1.8%。按照这个假设,北京的 数量为
假设这 1.8 万个 随机的分布在所有北京人口当中,那么你在北京随机遇到一个人,这个人是 的概率为
万分之七的概率看起来并不高,但这只是 的。
你变成 B 的概率有多大?
假如你住在北京,临近疫情期间前后并没有去过武汉。那么你逛街突然遇到一个 ,让你成为 ,这个概率有多大呢?假设所有人(包括潜伏期内的 )每周平均逛街 3 次,每次 1 小时。假设所有人会在早上 8 点到晚上 8 点这 12 个小时内逛街。因此,某个 出现在街上的概率为
因此早 8 点到晚 8 点这个时段中,某时刻同时在街上 的数量期望值为
因为你也每周上街 3 次,每次 1 小时。因此就有机会接触这 643 个 中的一个或多个人。我们假设“接触(相遇)”是指两人某时刻空间上的距离小于 3 米。假设所有人逛街的步行速度是 0.5 m/s,那么你每周逛街的这 3 个小时覆盖的总面积为
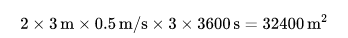
我们假设大家都在北京四环内逛,为什么假设是四环,主要是大模头我很少出四环,最远也就去过苏家坨。四环边长约为 18 公里,四环内面积约为 324 平方公里,假设商业及娱乐面积占 1%,因此你覆盖几率为
因此,你和某个 相遇的概率为 。你和所有 643 个 都不相遇的概率为
因此你和任意一个或多个 相遇的概率为
按照这一概率,春运结束 7 天后,北京将有 6.23 % 的人为 ,即
你变成 2B 的概率有多大?
春运结束 7 天后,北京疫情开始出现(潜伏期为 7 天)。所有 都被隔离,因此不会有新的 再出现。假设所有人都因为疫情减少了逛街的频率,改为一周逛街一次(买点必需品)。因此某个 出现在街上的概率为
因此早 8 点到晚 8 点这个时段中,同时在街上 的数量期望值为
因为你每周也逛街 1 个小时,你覆盖面积的几率为
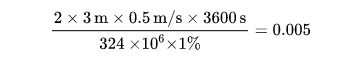
你和某个 相遇的概率为 ,因此你和所有 18534 个上街的 都不相遇的概率为
因此你和任意一个或多个 相遇的概率为
也就是说你逛一小时成为 的概率为 37.08 %。
结论
以下结论都建立在本文不太靠谱的假设前提下:
春运结束 7 天内,你逛街一个小时成为 的概率为 3.1 %。 春运结束 7 天后,你逛街一个小时成为 的概率高达 37 %。因此要少逛街,非要逛就带口罩。 本文没有计算 ,,,等其它各种情况。
本篇文章来源于微信公众号: 数学模型
推荐阅读:
版权声明:“备战深国交网”除发布相关深国交原创文章内容外,致力于分享国际生优秀学习干货文章。如涉及版权问题,敬请原作者原谅,并联系微信547840900(备战深国交)进行处理。另外,备考深国交,了解深国交及计划参与深国交项目合作均可添加QQ/微信:547840900(加好友时请标明身份否则极有可能加不上),转载请保留出处和链接!
非常欢迎品牌的推广以及战略合作,请将您的合作方案发邮件至v@scieok.cn本文链接:http://oxford.scieok.cn/post/800.html
-
- 申请真相|4个美国大学不小心拒掉你的理由
- 高考变难是趋势,选拔功能愈加突出,未来哪些考生会在高考中受益?
- 习近平:出国留学始终是培育人才的重要渠道,必须高度重视
- 美高留学费用惊人? 多个“热门留学地”花销大公开!
【算法 - 共抗疫情】北京不戴口罩在外1小时变成一“2B”人的概率
22695 人参与 2020年02月09日 21:18 分类 : 其它 评论
search zhannei
深国交2024年英美本科录取小计
-

未标注”原创“的文章均转载自于网络上公开信息,原创不易,转载请标明出处
深国交备考 |
如何备考深国交 |
深国交考试 |
深国交培训机构 |
备战深国交 |
联系方式
Copyright www.ScieOk.cn Some Rights Reserved.网站备案号:京ICP备19023092号-1商务合作
友情链接:X-Rights.org |中国校园反性骚扰组织 | 留学百词斩 | 南非好望角芦荟胶 | 云南教师招聘考试网 | 备战韦尔斯利网| 备战Wellesley




